A BAB 5 TRIGONOMETRI - Media Pembelajaran Namal Sparkly Santa Hat Ice Cream

TRIGONOMETRI Trigonometri (K13 Revisi) by   ahmadthohir1089 A. Satuan Ukuran Sudut Sebelumnya silahkan lihat arsip...

BAB 5 TRIGONOMETRI

BAB 5 TRIGONOMETRI

BAB 5 TRIGONOMETRI

8 10 99

TRIGONOMETRI


Trigonometri (K13 Revisi)


by 
A. Satuan Ukuran Sudut
Sebelumnya silahkan lihat arsip lama berikut ini:
Sebuah sudut akan terbentuk dari dua buah sinar yang berpotongan. Sedangkan sinar sendiri di sini adalah sebuah garis yang berpangkal pada sebuah titik dan memanjang ke suatu arah tertentu.
Perhatikanlah ilustrasi berikut
Dari ilustrasi gambar dua sinar di atas, antara sinar  \underset{OA}{\rightarrow}  dan sinar  \underset{OB}{\rightarrow}  bertemu di titik O sehingga terbentuklah sudut  \angle AOB.
Pada materi di tingkat SMP di kenalkan ukuran sudut dalam derajat dan radian. Selanjutnya secara singkat dapat dituliskan pada satu lingkaran penuh akan terdapat 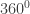 360^{0}atau 2\pi  radian.
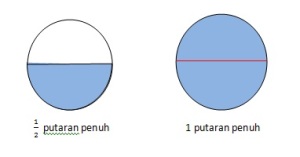
Coba perhatikan ilustrasi berikut!
Jika ditunjukkan dengan tabel ukuran sudutnya adalah sebagai berikut:
\begin{array}{|l|c|c|}\hline \quad\textrm{\textbf{Ukuran Sudut untuk}}&\textrm{\textbf{Derajat}}&\textrm{\textbf{Radian}}\\\hline \textrm{Satu Lingkaran Penuh}&360^{0}&\begin{matrix} 2\pi & rad \end{matrix}\\\hline \textrm{Setengah Lingkaran Penuh}&180^{0}&\begin{matrix} \pi & rad \end{matrix}\\\hline \textrm{Seperempat Lingkaran}&90^{0}&\begin{matrix} \displaystyle \frac{1}{2}\pi & rad \end{matrix} \\\hline \textrm{Seperlima lingkaran}&72^{0}&\begin{matrix} \displaystyle \frac{2}{5}\pi & rad \end{matrix}\\\hline \qquad\qquad\quad\quad\vdots &\vdots &\vdots \\\hline \qquad\qquad\quad\: \, dst&dst&dst\\\hline \end{array}.
Sebagai catatan ukuran sudut yang diubah ke menit dan/atau detik dinamakan sebagai sistem seksagesimal, yaitu:
\begin{aligned}1^{0}&=\begin{cases} {60}' & \text{dibaca} \: \: 60 \: \: \textrm{menit}\\\\ {3600}'' & \text{ dibaca } \: \: 3600\: \: detik \end{cases}\\\\ \textrm{in}&\textrm{gat}\: \, \: {1}'={60}''\: \: (\textrm{satu menit = 60 detik})\\ &\qquad 1^{0}={60}'=60\times {1}'=60\times {60}''={3600}'' \end{aligned}.
\LARGE\fbox{\LARGE\fbox{CONTOH SOAL}}.
\begin{array}{ll}\\ 1.&\textrm{Ubahlah ke dalam sudut-sudut berikut dalam radian}\\ &\begin{array}{llllllll}\\ \textrm{a}.&3^{0}&\textrm{e}.&90^{0}&\textrm{i}.&210^{0}&\textrm{m}.&300^{0}\\ \textrm{b}.&15^{0}&\textrm{f}.&120^{0}&\textrm{j}.&225^{0}&\textrm{n}.&315^{0}\\ \textrm{c}.&30^{0}&\textrm{g}.&135^{0}&\textrm{k}.&240^{0}&\textrm{0}.&12^{0}{24}'\\ \textrm{d}.&60^{0}&\textrm{h}.&150^{0}&\textrm{l}.&270^{0}&\textrm{p}.&30^{0}{12}'{30}'' \end{array}\\\\ &\textbf{Jawab}:\\ &\textrm{Ingat bahwa}:\quad 180^{0}=180\times 1^{0}=\pi \: rad\Rightarrow 1^{0}=\displaystyle \frac{\pi }{180}\: rad \\ &\begin{array}{|l|l|l|}\hline \begin{aligned}\textrm{a}.\quad 3^{0}&=\cdots \: \pi \: rad\\ 3^{0}&=\displaystyle \frac{3}{180}\pi \: rad\\ &=\displaystyle \frac{1}{60}\pi \: rad \end{aligned}&\begin{aligned}\textrm{c}.\quad 30^{0}&=\cdots \: \pi \: rad\\ 30^{0}&=\displaystyle \frac{30}{180}\pi \: rad\\ &=\displaystyle \frac{1}{6}\pi \: rad \end{aligned}&\begin{aligned}\textrm{f}.\quad 120^{0}&=\cdots \: \pi \: rad\\ 120^{0}&=\displaystyle \frac{120}{180}\pi \: rad\\ &=\displaystyle \frac{2}{3}\pi \: rad \end{aligned}\\\hline \begin{aligned}\textrm{m}.\quad 300^{0}&=\cdots \: \pi \: rad\\ 300^{0}&=\displaystyle \frac{300}{180}\pi \: rad\\ &=\displaystyle \frac{5}{3}\pi \: rad\\ &\\ &\\ &\\ & \end{aligned} &\multicolumn{2}{|c|}{\begin{aligned}\textrm{o}.\quad 12^{0}{24}'&=\cdots \: \pi \: rad\\ 12^{0}{24}'&=\displaystyle \frac{12+\left ( \displaystyle \frac{24}{60} \right )}{180}\pi \: rad\\ &=\displaystyle \frac{12+0,4}{180}\pi \: rad\\ &=\displaystyle \frac{12,4}{180}\pi \: rad\\ &=\displaystyle \frac{31}{450}\pi \: rad \end{aligned}}\\\hline \end{array} \end{array}.
\begin{array}{ll}\\ 2.&\textrm{Ubahlah ke dalam sudut-sudut berikut dalam derajat}\\ &\begin{array}{llllllll}\\ \textrm{a}.&\displaystyle \frac{1}{2}\pi \: rad&\textrm{e}.&\displaystyle \frac{4}{3}\pi \: rad\\\\ \textrm{b}.&\displaystyle \frac{3}{5}\pi \: rad&\textrm{f}.&2 \: rad\\\\ \textrm{c}.&\displaystyle \frac{2}{9}\pi \: rad&\textrm{g}.&12\: rad\\\\ \textrm{d}.&\displaystyle \frac{7}{12}\pi \: rad&\textrm{h}.&15\pi \: rad \end{array}\\\\ &\textbf{Jawab}:\\ &\textrm{Ingat bahwa}:\quad \pi \: rad=180^{0}\Rightarrow 1\: rad=\displaystyle \frac{180^{0}}{\pi } \\ &\begin{array}{|l|l|l|}\hline \begin{aligned}\textrm{a}.\quad \displaystyle \frac{1}{2}\pi \: rad&=\displaystyle \frac{1}{2}\pi \times \displaystyle \frac{180^{0}}{\pi }\\ &=90^{0} \end{aligned}&\begin{aligned}\textrm{b}.\quad \displaystyle \frac{3}{5}\pi \: rad&=\displaystyle \frac{3}{5}\pi \times \displaystyle \frac{180^{0}}{\pi }\\ &=108^{0} \end{aligned}&\begin{aligned}\textrm{d}.\quad \displaystyle \frac{7}{12}\pi \: rad&=\displaystyle \frac{7}{12}\pi \times \displaystyle \frac{180^{0}}{\pi }\\ &=105^{0} \end{aligned}\\\hline \multicolumn{3}{|c|}{\begin{aligned}\textrm{f}.\quad 2\: rad&=2\times \displaystyle \frac{180^{0}}{\pi }\\ &=2\times \displaystyle \frac{180^{0}}{\frac{22}{7}}\\ &=\displaystyle \frac{1260^{0}}{11}\\ &=114,\overline{54}\, ^{0} \end{aligned}}\\\hline \end{array} \end{array}
 

0 komentar:

Langganan: Posting Komentar (Atom)